LeetCode-N-Queens

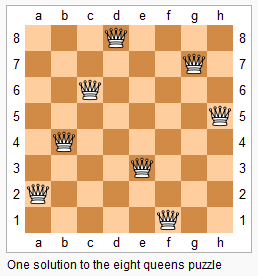
n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。
上图为 8 皇后问题的一种解法。
给定一个整数 n，返回 n 皇后不同的解决方案的数量。
注：皇后的攻击模式是同行或同列，以及两条斜线。

52 N-Queens N皇后

示例

输入: 4
输出: 2
解释: 4 皇后问题存在如下两个不同的解法。
[
 [".Q..",  // 解法 1
  "...Q",
  "Q...",
  "..Q."],

 ["..Q.",  // 解法 2
  "Q...",
  "...Q",
  ".Q.."]
]

思路

N皇后问题一直是一个很经典的问题。目前常见的算法多是递归加回溯，我先介绍一下这种递归加回溯的算法。
这种回溯加裁剪的思路，很像穷举，把所有路子走一遍，途中若走不通，就换一条路。
首先通过三个数组来判断当前位置是否能放皇后，一个是col，因为我们是按行遍历的，所以只需要考虑列是否被占用，isDiagonal[]是正对角线，obliqueDiagonal[]是斜对角线，然后根据条件遍历裁剪即可。

public class NQueens {
    //列，某一列是否被占用
    int[] col;
    //正对角线
    int[] isDiagonal;
    //斜对角线
    int[] obliqueDiagonal;
    public static void main(String[] args) {
        int result = new NQueens().totalNQueens(8);
        System.out.println(result);
    }

    /**
     * 初始化
     *
     * @param n 皇后数
     * @return
     */
    public int totalNQueens(int n) {
        col = new int[n];
        isDiagonal = new int[2 * n - 1];
        obliqueDiagonal = new int[2 * n - 1];
        return putQueen(n, 0);
    }

    /**
     * 开始放置皇后
     *
     * @param n        总皇后数
     * @param queenNum 已放置皇后数
     * @return
     */
    public int putQueen(int n, int queenNum) {
        int result = 0;
        if (queenNum == n) {
            return 1;
        }
        for (int i = 0; i < n; i++) {
            //判断是否能放皇后
            if (col[i] == 0 && isDiagonal[queenNum - i + n - 1] == 0 && obliqueDiagonal[queenNum + i] == 0) {
                //皇后放在此处，并标记此皇后攻击的点
                col[i] = 1;
                isDiagonal[queenNum - i + n - 1] = 1;
                obliqueDiagonal[queenNum + i] = 1;
                result += putQueen(n, queenNum + 1);

                //解除标记，继续移动皇后
                col[i] = 0;
                isDiagonal[queenNum - i + n - 1] = 0;
                obliqueDiagonal[queenNum + i] = 0;
            }
        }
        return result;
    }
}